Grafik Modeli tanıma, herhangi bir tüccarın Teknik Analizde geliştirdiği temel ve birincil yetenektir. Temel bir gelişme olabilir, ancak örüntü tanımanın mükemmelliği, kapsamlı uygulama ve tekrarlayan maruz kalma gerektirir. Kalıpların uzman tarafından tanınması, tüccarların değişen piyasa ortamını ölçmelerine ve bunlara tepki vermelerine yardımcı olur. Grafik kalıpları, ayrıca basit ve karmaşık kalıplar olarak sınıflandırılan “sürekli” ve “ters” kalıplar olarak kategorize edilir. Karmaşık kalıp yapıları, basit kalıp koleksiyonlarından ve önceki dalgalanmaların kombinasyonundan oluşabilir. Bu örüntü tanıma sınıflandırması ve özellikleri hakkında bilgi, tüccarlara daha geniş bir ticaret koşullarına tepki verme ve uyum sağlama konusunda daha fazla potansiyel sağlar.
Piyasa fiyatları her zaman trend, konsolidasyon ve yeniden trend davranışı sergiler. Tek bir çubukta önceki bir trendden dönmek için trendlerini ve geçiş aşamalarını nadiren tersine çevirir. Bu geçiş aşamasında, ticaret aralıkları ve fiyat dalgalanmaları yaşarlar. Bu değişen eylem, tanımlanabilir fiyat modellerini tanımlar. Bu konsolidasyon aşamaları, zaman zaman, oluşumlarından önceki hakim eğilimleri destekler ve yönlerini sürdürür. Bunlara “devam” kalıpları denir. Bu kalıplara örnek olarak Simetrik Üçgen , Bayraklar ve Kupa ve Kulp verilebilir . Bazı aşamalar, önceki eğilimin tersine çevrilmesi ve yeni yönde devam edilmesiyle sonuçlanır. Bunlara “ters çevirme” kalıpları denir. Bu modellerin örnekleri arasında Baş ve Omuzlar bulunur, Çift Dipler ve Genişleyen Modeller .
Harmonik Modeller kavramı, 1932’de HM Gartley tarafından oluşturuldu. Gartley, Karlar Borsasında 5 noktalı bir model (Gartley olarak bilinir) hakkında yazdı . Larry Pesavento, Fibonacci Ratios with Pattern Recognition adlı kitabında bu modeli Fibonacci oranlarıyla geliştirdi ve “Gartley” modelinin nasıl ticaret yapılacağına dair kurallar belirledi . Bu örüntü teorisi üzerinde çalışan birkaç başka yazar var, ancak bildiğim kadarıyla en iyi çalışma Scott Carney tarafından “Harmonik Ticaret” kitaplarında yapıldı. Scott Carney ayrıca “Yengeç”, “Yarasa”, “Köpekbalığı” ve “5-0” gibi kalıplar icat etti ve ticaret kuralları, geçerliliği ve risk/para yönetimi için gerçek derinlikte bilgi ekledi.
Harmonik kalıpların arkasındaki birincil teori, Fibonacci oran ilişkilerine ve piyasalardaki simetrisine uyan fiyat/zaman hareketlerine dayanmaktadır. Fibonacci oranı analizi, herhangi bir pazarda ve herhangi bir zaman çizelgesi tablosunda iyi çalışır. Bu oranları kullanmanın temel fikri, bir dizi yüksek ve düşük salınım noktaları ile birlikte önemli dönüm noktalarını, düzeltmeleri ve uzantıları belirlemektir. Bu dalgalanma noktalarını (En Yüksekler ve En Düşükler) kullanan türetilmiş tahminler ve düzeltmeler, Hedefler veya Duraklar için temel fiyat seviyelerini verecektir.
Harmonik modeller, Fibonacci dizilerini kullanarak geometrik model yapıları (geri çekilme ve izdüşüm salınımları/bacakları) oluşturur. Belirtilen (harmonik) kalıplar olarak tanımlanan bu harmonik yapılar, tüccarlar için potansiyel fiyat hareketleri ve önemli dönüş veya trend tersine çevirme noktaları gibi benzersiz fırsatlar sağlar. Harmonik kalıplar fiyat girişleri, stoplar ve hedef bilgileri hakkında oldukça güvenilir bilgiler sağlamaya çalıştıklarından, bu faktör tacirler için bir avantaj sağlar. Bu, diğer göstergeler/osilatörler ve nasıl çalıştıkları ile önemli bir farklılaşma olabilir.
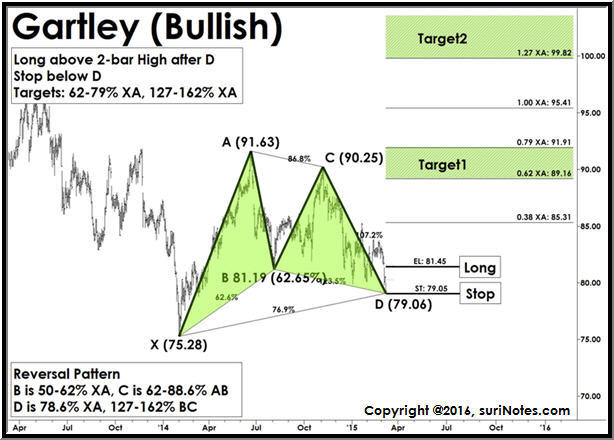
Aşağıda gösterilen Gartley paterni, 5 puanlık bir yükseliş formasyonudur. Bu modeller “M” veya “W” desenlerine benzer ve 5 temel pivot noktası ile tanımlanır. Gartley desenleri, 5 noktalı bir desen oluşturan 2 geri çekme ayağı ve 2 impuls sallanan bacaktan oluşur. Tüm bu dalgalanmalar birbiriyle ilişkilidir ve Fibonacci oranlarıyla ilişkilidir. Modelin merkezi (göz), modeli tanımlayan “B”, “D” ise işlemlerin yapıldığı eylem veya tetikleme noktasıdır. Model, “D” seviyesinden ticarete giriş, durdurma ve hedef seviyelerini gösterir.
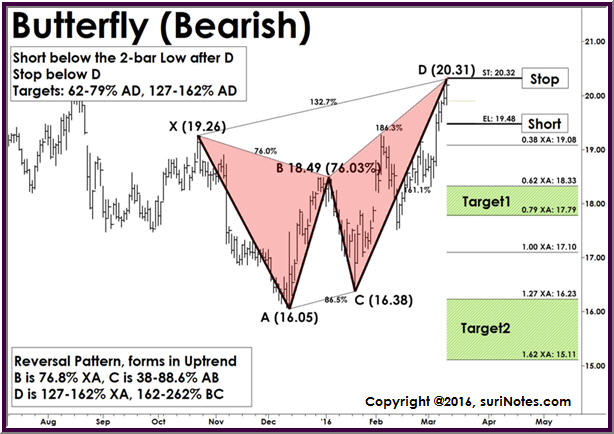
Aşağıdaki grafik, başka bir 5 noktalı harmonik modeli (Kelebek Ayı) göstermektedir. Bu model, yukarıdaki 5 noktalı Gartley modeline benzer, ancak tersidir. Burada desen, “B” desenin merkezi (göz) olmak üzere “W” şeklindedir. Model, “XA” ayağı kullanılarak “D” seviyelerinden ticarete giriş, durdurma ve hedef seviyelerini gösterir.
Harmonik modeller hakkındaki herhangi bir tartışma Fibonacci sayılarını içermelidir, çünkü bu modeller Fibonacci oranlarını kapsamlı bir şekilde kullanır. Fibonacci sayıları evrende yaygındır ve orijinal olarak Leonardo Fibonacci tarafından türetilmiştir. Temel Fibonacci oranı veya “Fib oranı” Altın Oran’dır (1.618). Fibonacci sayıları, her sayının önceki iki sayının toplamı olduğu bir sayı dizisidir.
Fib Sayıları dizisi şu şekilde başlar: 1,1,2,3,5,8,13,21,34,55,89,144,233,317,610….
Bu sayıların doğada ve finans dünyasında nasıl var olduğuna dair teori hakkında pek çok materyal ve kitap var. Gerçek Fibonacci dizisinin karesini alarak, karekökünü alarak ve ileri geri hareket ettirerek elde edilen, finans dünyasındaki en önemli Fib oranlarının bir listesi aşağıda gösterilmiştir.
Ticarette Fibonacci’den türetilen oranların anahtar seti: 0.382, 0.618, 0.786, 1.0, 1, 1, 2.0, 2.62, 3.62, 4.62
Alım satımda ikincil Fibonacci türevi oranlar seti: 0.236, 0.886, 1.13, 2.236, 3.14, 4.236
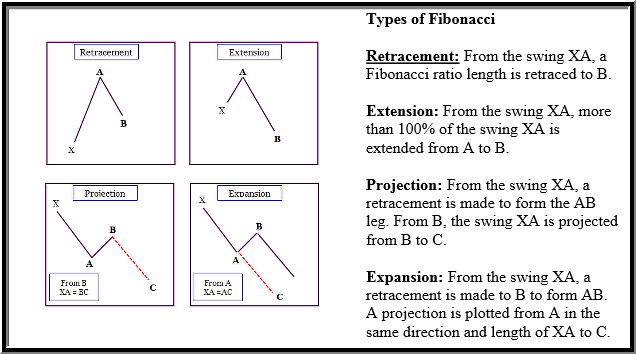
Teknik analizde Fibonacci’nin birçok uygulaması vardır. Uygulamalardan bazıları, diğerleri arasında Fibonacci düzeltmeleri, Fibonacci projeksiyonları, Fibonacci Hayranları, Fibonacci Yayları, Fibonacci Zaman Dilimleri ve Fibonacci Fiyat ve Zaman Kümelerini içerir.
Çoğu ticari yazılım paketi, Fibonacci düzeltmelerini, uzantılarını ve tahminlerini gösterebilen Fibonacci çizim araçlarına sahiptir. Ek olarak, Fibonacci sayıları ticarette “zaman” ve “fiyat” için de uygulanabilir.
Aşağıdaki grafik, Fibonacci oranlarının düzeltme, uzatma, projeksiyon ve genişleme dalgalanmalarını uygulamak için nasıl kullanıldığını göstermektedir.
Harmonik kalıpları çıplak gözle tespit etmek biraz zor olabilir, ancak bir tüccar kalıp yapısını anladığında, Fibonacci araçları tarafından nispeten kolayca tespit edilebilir. Birincil harmonik modeller 5 noktalı (Gartley, Kelebek, Yengeç, Yarasa, Köpekbalığı ve Cypher) kalıplardır. Bu kalıplar gömülü 3 noktalı (ABC) veya 4 noktalı (ABCD) kalıplara sahiptir. Bu noktalar arasındaki tüm fiyat dalgalanmaları birbiriyle ilişkilidir ve Fibonacci’ye dayalı harmonik oranlara sahiptir. Modeller ya “M” ya da “W” şeklindeki yapıları ya da “M” ve “W” kombinasyonlarını oluşturuyor ya da tamamlamış durumda. Harmonik paternler (5-nokta), AB ayağını tamamlayan (B)’de “EYE”yi oluşturmak için bir kritik orijine (X) ve ardından bir itme dalgasına (XA) ve ardından bir düzeltici dalgaya sahiptir. Ardından bir trend dalgası (BC) gelir ve son olarak bir düzeltici bacak (CD) ile tamamlanır. Bu bacaklar arasındaki kritik harmonik oranlar, bir modelin adının (Gartley, Butterfly, Crab, Bat, Shark ve Cypher) yanı sıra geri çekilme tabanlı mı yoksa uzantı tabanlı bir model mi olduğunu belirler. Hatırlanması gereken önemli noktalardan biri, tüm 5 noktalı ve 4 noktalı harmonik modellerin gömülü ABC (3 Noktalı) modellere sahip olmasıdır.
Tüm 5 noktalı harmonik modeller (Gartley, Kelebek, Yengeç, Yarasa, Köpekbalığı, Cypher) benzer prensiplere ve yapılara sahiptir. Bacak uzunluk oranları ve anahtar düğümlerin konumları (X, A, B, C, D) açısından farklılık gösterseler de, bir modeli anladığınızda diğerlerini anlamak nispeten kolay olacaktır. Kalıpları bulmak veya zorlamak için çıplak gözle kullanmak yerine, tüccarların bu kalıpları tanımlamak için otomatik bir kalıp tanıma yazılımı kullanmasına yardımcı olabilir.
Örnek: Aşağıdaki grafik, gömülü ABC Ayı formasyonuna sahip Yarasa Boğa formasyonunun bir örneğini göstermektedir. Tanımlama pivotları ve oranları model üzerinde işaretlenmiştir; model aynı zamanda giriş, durma ve hedef seviyelerini de gösterir.
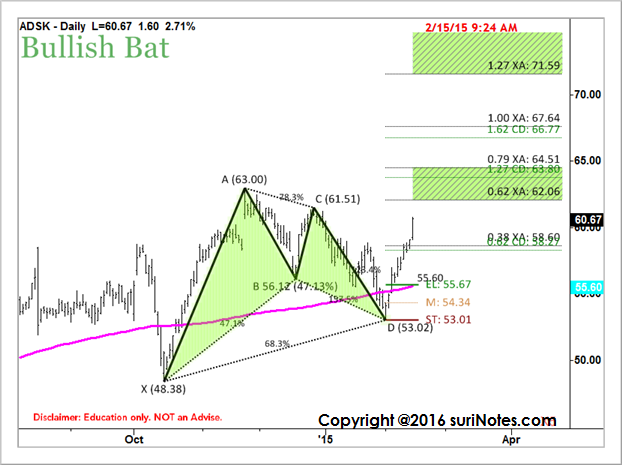
Harmonik kalıp kurulumlarında, ilk 3 ayak tamamlandığında (5 noktalı kalıplarda) bir ticaret tanımlanır. Örneğin, Gartley Boğa formasyonunda, XA, AB ve BC ayakları tamamlanır ve CD ayağını oluşturmaya başlar, olası bir ticaretin iş başında olduğunu tespit edersiniz. Fibonacci oranlarıyla birlikte XA ve BC bacaklarının projeksiyonlarını ve geri çekilmelerini kullanarak, modelin potansiyel bir Model Tamamlama Bölgesi (PCZ) ve D noktasını belirlemek için bir fiyat kümesi oluşturabiliriz.
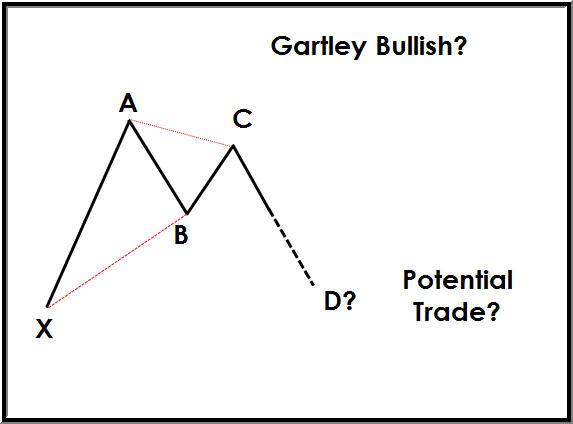
Tüm harmonik modeller, tanımlanmış Model Tamamlama Bölgelerine (PCZ) sahiptir. Fiyat kümeleri olarak da bilinen bu PCZ’ler, Fibonacci uzantılarının, geri çekilmelerin ve fiyat tahminlerinin tamamlanmış salınım (bacaklar) birleşiminden oluşur. Kalıplar genellikle CD ayağını PCZ’de tamamlar, sonra tersine döner. Alım satımların bu bölgede olması bekleniyor ve fiyat tersine çevirme eylemine girildi.
Örnek olarak, Boğa Gartley formasyonunun Model Tamamlama Bölgesi (PCZ), aşağıdaki Fibonacci uzantıları ve tahminleri kullanılarak oluşturulur:
0,78 XA
MÖ 1.27
MÖ 1.62
AB = CD
Aşağıda, idealleştirilmiş Potansiyel Tamamlama Bölgesi (PCZ) oluşumunun bir örneği verilmiştir:
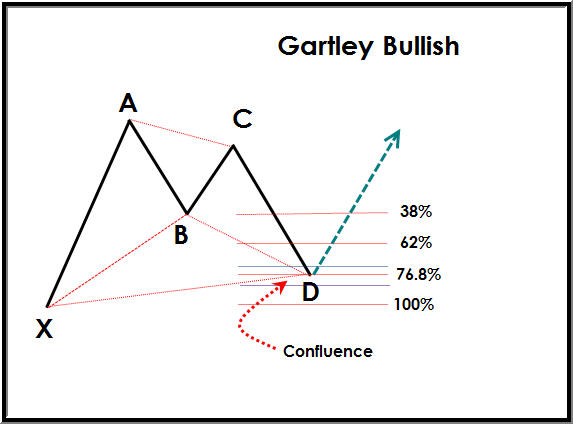
Aşağıda, gerçek dünyadaki Potansiyel Tamamlama Bölgesi (PCZ) oluşumuna bir örnek verilmiştir:
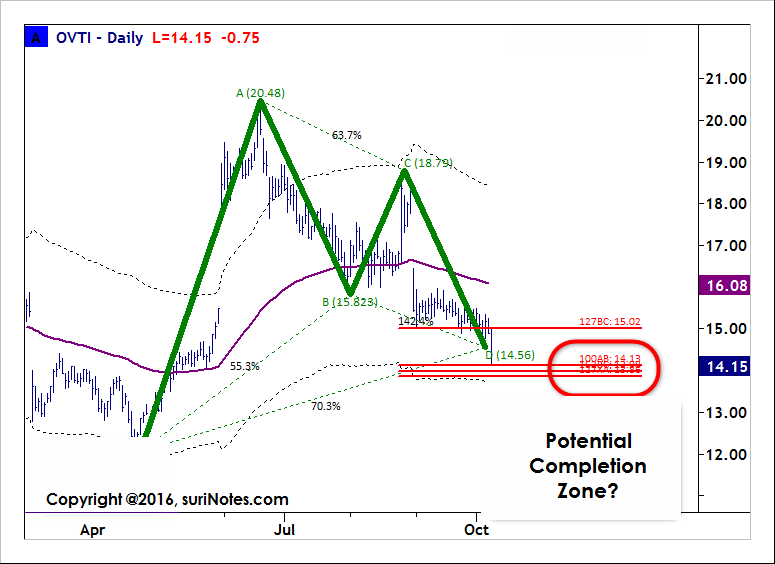
Çoğu teknik tüccar, ticaret yapmak için piyasa bağlamı kavramlarıyla grafik analizini kullanır. Piyasa bağlamı kavramı, mevcut fiyatın belirli seviyelere nasıl tepki verdiği (pivotlar, destek ve direnç, MA’lar), göstergelerin geçmiş fiyat koşullarına göre nasıl performans gösterdiği (aşırı satış, aşırı alım gibi) ve mevcut zaman diliminde modellerin nerede/nasıl geliştiği olarak tanımlanır. veya çoklu zaman dilimleri vb. Her tüccar, ticaret yapmak için kendi piyasa bağlamını geliştirir. Pazar bağlamını tanımlamanın zarif yollarından biri, bir Fibonacci Grid yapısıdır. Fibonacci Izgarası, Fibonacci bantlarından (fiyat reaksiyonunu, trendleri gösteren), pivot seviyelerinden (tarihi Destek/Direnç alanlarını göstermek için) ve Piyasa Yapılarından (potansiyel dönüm noktalarını göstermek için) oluşur. Herhangi bir ticaret tablosunda,
Bu seviyelerin Fibonacci Grid yapısındaki birleşimi, ortaya çıkan model yapısı (ve model hedef/durdurma seviyeleri) ile birlikte, bir tüccarın iyi bir karar vermesine yardımcı olur. Model ticareti, her modelin belirli giriş/durdurma kuralları ve hedefleri olduğu için çok kesindir. Harmonik örüntü analizi ve piyasa bağlamı birleştirildiğinde, ticarette büyük bir avantaj sağlar. Harmonik kalıplar başarısız olabilir, ancak başarısızlık seviyeleri iyi tanımlanmıştır ve bu bilgi ticaretten önce açıkça bilinmektedir. Bu nedenle, Harmonik model ticaretinin diğer ticaret yöntemlerinden çok daha fazla olumlu yönü vardır.
Diğer piyasa bağlamı/onay koşulları ve göstergeleri arasında Sapma, Çoklu Zaman Çerçeveleri, Fibonacci Bantları, Andrew Dirgen Analizi, Hareketli Ortalamalar, Pivotlar, Kanallar, Eğilim Çizgileri, Hacim ve Oynaklık yer alır.
Örnek: Aşağıdaki örnek, Model analizi ile Pazar Bağlamının nasıl kullanıldığını gösterir. Bu örnek, AAPL’nin (tarih: 07 Şubat 2014) 200-SMA üzerinde ve Fibonacci Bantlarının (A, C noktaları) dışında bir Boğa Yengeç formasyonunu oluşturduğunu ve Yengeç formasyonuna sahip alt Fibonacci Bantlarının yakınında bir D noktasının oluştuğunu göstermektedir. Ayrıca, orta Fibonacci bandı seviyesinin altında işlem gören ve potansiyel bir tükenme kurulumuna işaret eden alt Fibonacci bandına yakın işlem gören modele dikkat edin. Boğa Yengeç kurulumunu tamamladıktan sonra, kuruluma Uzun bir girişin sinyalini vermek için fiyat EL’in üzerinde işlem gördü. Fiyat eğimi 200-SMA’nın üzerinde pozitif olduğu için AAPL’nin genel eğilimi de yükseliş gösteriyor. 07 Şubat 2014’te, 70.50’nin (-3.21) altında Durdurma ile 73.71’in üzerinde bir Uzun yükseliş ticaretine girildi. Hedef seviyeler, Hedef Bölge 1 için 77,7 ila 79,7, Hedef Bölge 2 için 85,3 – 89,4’tür.
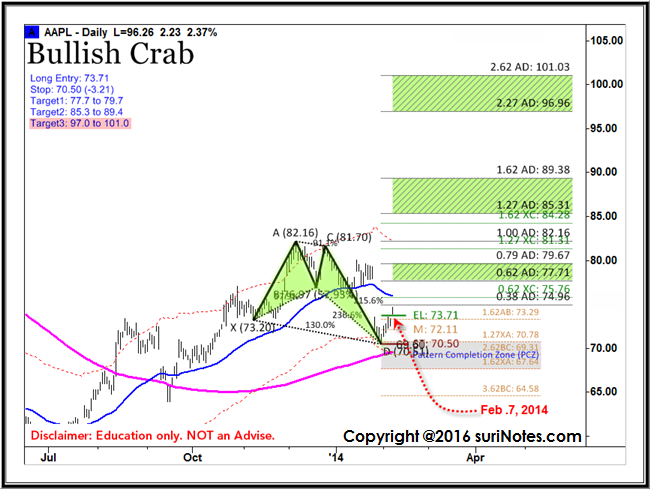
Aşağıdaki tablo (9 Haziran 2014), AAPL Boğa Yengeç modeli ilerlemesini ve hedeflerin tamamlanmasını göstermektedir.
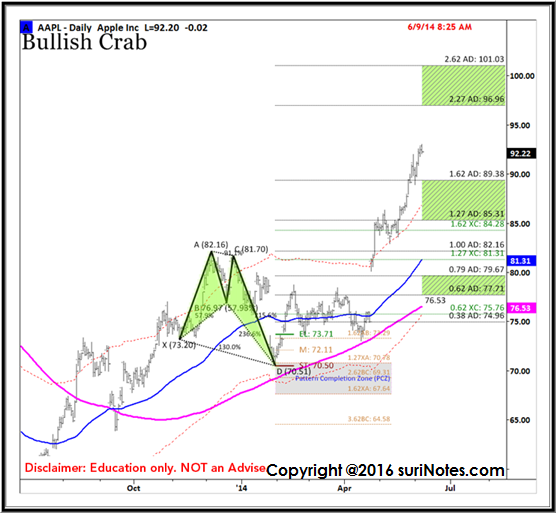
Harmonik kalıpları hesaplanmış giriş seviyeleriyle ticaret yapmak, bunları harmonik ticaret uzmanları tarafından savunulan düzeltme seviyelerinde veya ters bölgelerde körü körüne ticaret yapmaktan ziyade bu yazarın tercihidir. Çoğu harmonik tüccar, modelin tersine döneceğini tahmin eder ve bu modelleri “tersine dönüş bölgesinde” ticaret yapmaya çalışır ve sonunda karşıt (karşı trend) işlemler yapar. Bir ticarete girmek için, “ters bölgelerden” bir ters trend değişikliği ile birlikte fiyat hareketinin tersine çevrildiğinin onaylanmasını tercih ederim.
Harmonik model ticaret girişlerinin çoğu, ters bölge içindeki “D” noktası civarında gerçekleşir. Bu bir Alış (yükselen formasyonlarda) veya bir Satış (düşen formasyonlarda) olabilir. Genellikle “D”, evrensel olarak “ters bölge” olarak adlandırılan önceki salınımların (bacaklar) projeksiyonlarının, geri çekilmelerinin ve uzantılarının bir araya gelmesiyle tanımlanır. Benim görüşüme göre, fiyatların bu bölgeye ulaşmaya başlaması, henüz bir ticaret sinyali değil, potansiyel bir ticaret fırsatı sinyali veriyor. Giriş kriterleri ve kalıp geçerliliği, mevcut oynaklık, altta yatan trend, model içindeki hacim yapısı ve piyasa iç değerleri vb. seviyeleri (EL), fiyat aralıkları, oynaklık veya bazı kombinasyonlar kullanılarak hesaplanabilir.
Harmonik modellerdeki hedef bölgeler, model yapısının hareket noktasından gelen impuls/düzeltici salınımların ve Fibonacci oranlarının geri çekilmesine, uzantılarına veya izdüşümlerine dayalı olarak hesaplanır. Örneğin, Gartley yükseliş modelinde hedef bölgeler, ticari işlem noktasından (D) XA ayağı kullanılarak hesaplanır. Projeksiyonlar, XA ayağının %62 veya %78,6’sı gibi Fibonacci oranları kullanılarak hesaplanır ve eylem noktasına (D) eklenir. Potansiyel hedef seviyeleri için 1., 1.27, 1.62, 2., 2.27 veya 2.62 gibi genişleme oranları hesaplanır. Birincil hedef bölgeler, XA ayağının %62 – %78,6’sı birinci hedef bölge ve %127 – %162’si ikinci hedef bölge olacak şekilde D’den hesaplanır.
Hedef Bölge 1: (D + XA*0,62) ila (D+XA*,786)
Hedef Bölge 2: (D + XA*1,27) ila (D+XA*1,62)
Harmonik modellerdeki potansiyel hedef bölgelerin mutlak kesinlikle değil, olasılık açısından hesaplandığını not etmek önemlidir. Herhangi bir model ticaret başarısı için güçlü para ve risk yönetimi kuralları ve modelin tam çalışma bilgisi gereklidir.
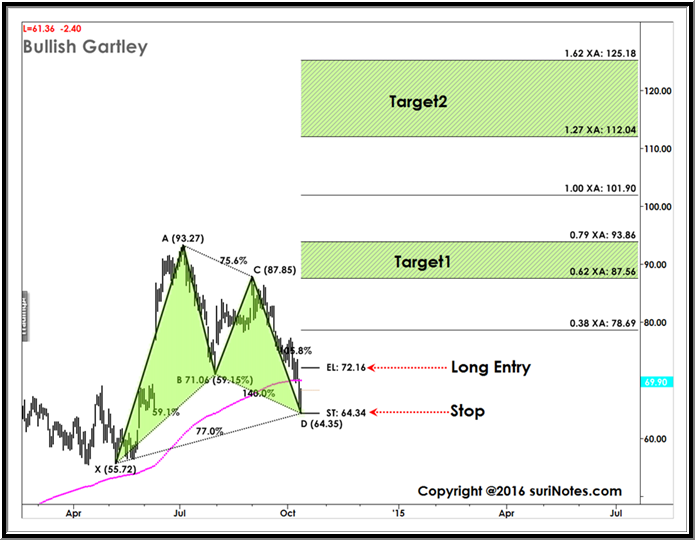
Örnek: Aşağıdaki grafik, giriş seviyesi, durakları ve hedef bölgeleri olan bir Boğa Gartley Modelini göstermektedir. Hedef bölgeler, D’den XA salınım uzunluğu ve Fibonacci oranları kullanılarak tahmin edilir. Hedef Bölge 1, %62 – %79 aralığını kapsarken, Hedef Bölge 2, %127 ila %162 arasındadır.
kaynak : https://school.stockcharts.com/
| Dolar | 37,9223 | % -0.07 |
| Euro | 41,0105 | % -0.05 |
| Sterlin | 49,1219 | % -0.07 |
| Bitcoin | 3212282,00 | % 0.77 |
| Ethereum | 70973,00 | % 0.40 |
| Çeyrek | 6.281,00 | % -0,13 |
| G. Altın | 3.806,91 | % 0,21 |
| BIST 100 | 9.575,96 | % -0,86 |
| Litecoin | 3134.6 | % -1.90 |
| B. Cash | 11596.72,00 | % -2.17 |